‘Sup
Look, I’m sorry. Yet again, I’ve not written any blog posts for ages. Let’s all get over it and move on to something more important. Sales. Let’s imagine you’re an organisation selling B2B. You use Salesforce (or any other platform). You’ve got plenty of opportunities and a history of those opportunities. You’ve gone and built a sales pipeline.
Good work. That’s not an easy thing to do.
Now you want to use that pipeline to get better at sales. You want to use the data you’ve got to help forecast what you’ll do in the future. You want to know the value of what you’ve already got in the pipeline. You want to know what the most valuable activities you perform are. I’m not going to be able to fit all of that into one post so I’ll break things up into parts and (I’ve said this before only to underdeliver) FINISH THE SERIES.
However, for part 1 I’m actually only going to focus on generating some dummy data to play with. “What!? That’s none of the things you said you’d do!” No. It’s not. However, if you’re able to find me a B2B company with a small number of sales who are willing to publicly share all their data then fair play to you. Lacking that I’m going to have to create a dummy set of data and make it halfway believable. In doing this I’ve made a few assumptions (that I’m later going to try to show). It’s a bit circular but don’t be that guy. What I’m doing is broadly legit and if you look at the data and don’t think it’s reasonable then I’m providing the code so you can change whichever bit you find egregious. Even better, just use your actual company’s sales data (assuming you’re lucky enough to have it).
I’ll be building a dataframe that resembles a Salesforce pipeline – it’s going to have the following rows:
Stage – this is the ‘Salesforce/Hubspot/<don’t care>’ stage in the pipeline. Measures how far along an opportunity is.
Name – got to keep track of the opportunities using something
Value – how much money are we going to make from this opportunity. Daily, Monthly, Annually. Doesn’t matter.
Days – this is the date the opportunity entered the stage given. Going to be important later for time-dependence stuff.
So, let’s begin (all code also available here)
import numpy as np
import random
import matplotlib
from matplotlib import pyplot as plt
import datetime
from datetime import datetime as dt
from scipy import stats
import pandas as pd
def weighted_pick(weights, n_picks):
t = np.cumsum(weights)
s = np.sum(weights)
return np.searchsorted(t, np.random.rand(n_picks)*s)
pre_stages = [('Contact initiated', 0.8, 10), ('Meeting booked', 0.6, 20), ('Trial booked', 0.4, 15), ('Proposal sent', 0.3, 25), ('Contract sent', 0.2, 10)]
closed_stages = ['Closed Won', 'Closed Lost']
success_stages = ['Closed Won']
Here I’m declaring a few things that are going to be useful to me later. I want all of the stages in the pipeline that I care about, the closed stages and the success stages. The code is probably a bit brittle regarding the random addition of closed and success stages but is fine for new ‘pre_stages’. The parameters are the probability that the opportunity will fall out of this stage (rather than move on successfully) and something else that we’ll talk about later.
WORDS = open('/usr/share/dict/words', 'rb').read().splitlines()
NUM_POINTS = 400
AVERAGE_SALE_PRICE = 3500
SD_SALE_PRICE = 1000
sales_opportunities = [(entry.title(), np.random.normal(AVERAGE_SALE_PRICE, SD_SALE_PRICE)) for entry in np.random.choice(WORDS, NUM_POINTS, replace=False)]
Here I’m generating a list of ‘company names’, picking words randomly from a dictionary. In all honesty, just looking through the list of company names is pretty fun in itself. I’m also assuming that the revenue I make from my product is a normal distribution with mean and standard deviation given as ‘AVERAGE_SALE_PRICE’ and ‘SD_SALE_PRICE’. Not rocket science. But it is an assumption I’m making – let’s chalk it down. First assumption: revenue/client is normally distributed. Then we build a list of sales opportunities and their value.
start_date = datetime.datetime.now() - datetime.timedelta(days = 365*2)
days_range = range(365*2)
y = [float(entry)/365. for entry in days_range]
indices = weighted_pick(np.exp(y), NUM_POINTS)
Second assumption I’m going to make in generating this data – you’re working for the right kind of start-up/business. Basically, the number of opportunities created are going to broadly follow an exponential distribution. That is, you specify how many opportunities enter the pipeline with ‘NUM_POINTS’ and we’re going to distribute those according to an exponential distribution. I’m saying that the company starts 2 years ago – again, change if you don’t like it.
sales_data = [[pre_stages[0][0], name_value_pair[0], name_value_pair[1], start_date + datetime.timedelta(days = index)] for name_value_pair, index in zip(sales_opportunities, indices)]
remaining_opportunities_frame = pd.DataFrame(sales_data)
remaining_opportunities_frame.columns = ['Stage', 'Name', 'Value', 'Days']
sales_data_frame = pd.DataFrame(sales_data)
sales_data_frame.columns = ['Stage', 'Name', 'Value', 'Days']
finished_list = set([])
OK. Now I’ve got the first set of entries that’ll make up my final dataframe – it’s all of the opportunities with the value (generated from a normal distribution) and the time the opportunity entered the pipeline (generated via an exponential distribution). I’m going to create a few things for later, namely a dataframe containing all of the live opportunities and our final dataframe containing all the rows we’re going to care about.
for stage_index, stage in enumerate(pre_stages[1:]):
next_stage = pd.DataFrame([(sales_opp[1], index, np.argmax(entry)) for sales_opp in sales_data for index, entry in enumerate(np.random.multinomial(1, [0.99, (1. - stage[1])/100., stage[1]/100.0], (datetime.datetime.now() - sales_opp[3]).days)) if entry[0] != 1 and sales_opp[1] not in finished_list])
The above line is where it’s all at. Let me explain slowly and then again, even slower. My intuition is this – I think that the probability that an opportunity converts (moves from its current stage to the next stage) is proportional to the negative exponential of the time spent in that stage. Let’s be clearer. I’m going to make the third assumption – that the probability of moving to the next stage broadly follows a negative exponential. What’s more, I think that each stage will have its own characteristic drop off rate (or half-life, for those of you thinking this looks mightily like radioactive decay). You know how before I said I’d added a parameter to ‘pre_stages’ and I’d explain it. That’s what ‘pre_stages[x][2]’ is. So, for a given stage in the sales pipeline, for each opportunity left in the previous stage, for every day between when the opportunity entered the stage and now I run the multinomial line. The multinomial line is going to return a binary array of three elements where exactly one of the elements is filled. The first element will be filled in 99% of cases – I’ve chosen to set this and if you don’t like it then change it to something else. It means that, for every day between the opportunity entering the state and today there’s a 99% the opportunity will still be in that state at the end of the day. If the second element is filled then that means that the opportunity succeeded on that particular day (with probability given by the stage parameter). Finally, if the third element is filled then the opportunity died on that particular day. ‘Index’ gives us the number of days that’ve happened since the opportunity entered the stage and the argmax gives us whether we succeeded or failed (you’ll see we’re ignoring days when we neither succeeded or failed).
next_stage.columns = ['Name', 'Days', 'Status']
meh = next_stage.ix[next_stage.groupby('Name').Days.idxmin()]
tempy_frame = meh.merge(remaining_opportunities_frame[['Name', 'Value', 'Days']], how='inner', on='Name')
tempy_frame['new_date'] = tempy_frame.apply(lambda x: x.Days_y + datetime.timedelta(days = x.Days_x), axis=1)
tempy_frame = tempy_frame[['Name', 'Value', 'new_date', 'Status']]
tempy_frame.columns = ['Name', 'Value', 'Days', 'Status']
success_frame = tempy_frame[tempy_frame.Status == 1]
success_frame = success_frame.drop('Status', 1)
success_frame.insert(0, 'Stage', pre_stages[stage_index + 1][0] if stage_index + 1 < len(pre_stages) - 1 else success_stages[0])
failure_frame = tempy_frame[tempy_frame.Status == 2]
failure_frame = failure_frame.drop('Status', 1)
failure_frame.insert(0, 'Stage', closed_stages[1])
sales_data_frame = sales_data_frame.append(success_frame).append(failure_frame)
That was a crazy line – but it contained most of the interesting stuff we do. From here on in we grab the first of the days that the opportunity moved (we actually kept all of the days in the above line but we’re only allowing each opportunity to move out of each stage once!), add the number of days to the original date we entered the stage to find the day we move into the next stage and then create the rows that we need.
finished_frame = sales_data_frame.groupby('Name').apply(lambda x: x.Stage.isin(closed_stages).any())
finished_list = set(finished_list).union(set(finished_frame[finished_frame == True].index.values))
remaining_opportunities = remaining_opportunities_frame[~remaining_opportunities_frame.Name.isin(finished_list)]
Finally, there’s a bit of tidying up to make sure that we don’t calculate anything for any of the opportunities that have died
dates = matplotlib.dates.date2num(sales_data_frame[sales_data_frame.Stage == success_stages[0]].sort('Days').Days.astype(dt))
revenue = sales_data_frame[sales_data_frame.Stage == success_stages[0]].sort('Days').Value.cumsum().values
plt.plot_date(dates, revenue, 'b-')
plt.xlabel('Date')
plt.ylabel('Revenue')
plt.title('Company revenue over time')
plt.show()
sales_data_frame.to_csv('generated_data.csv', index=False)
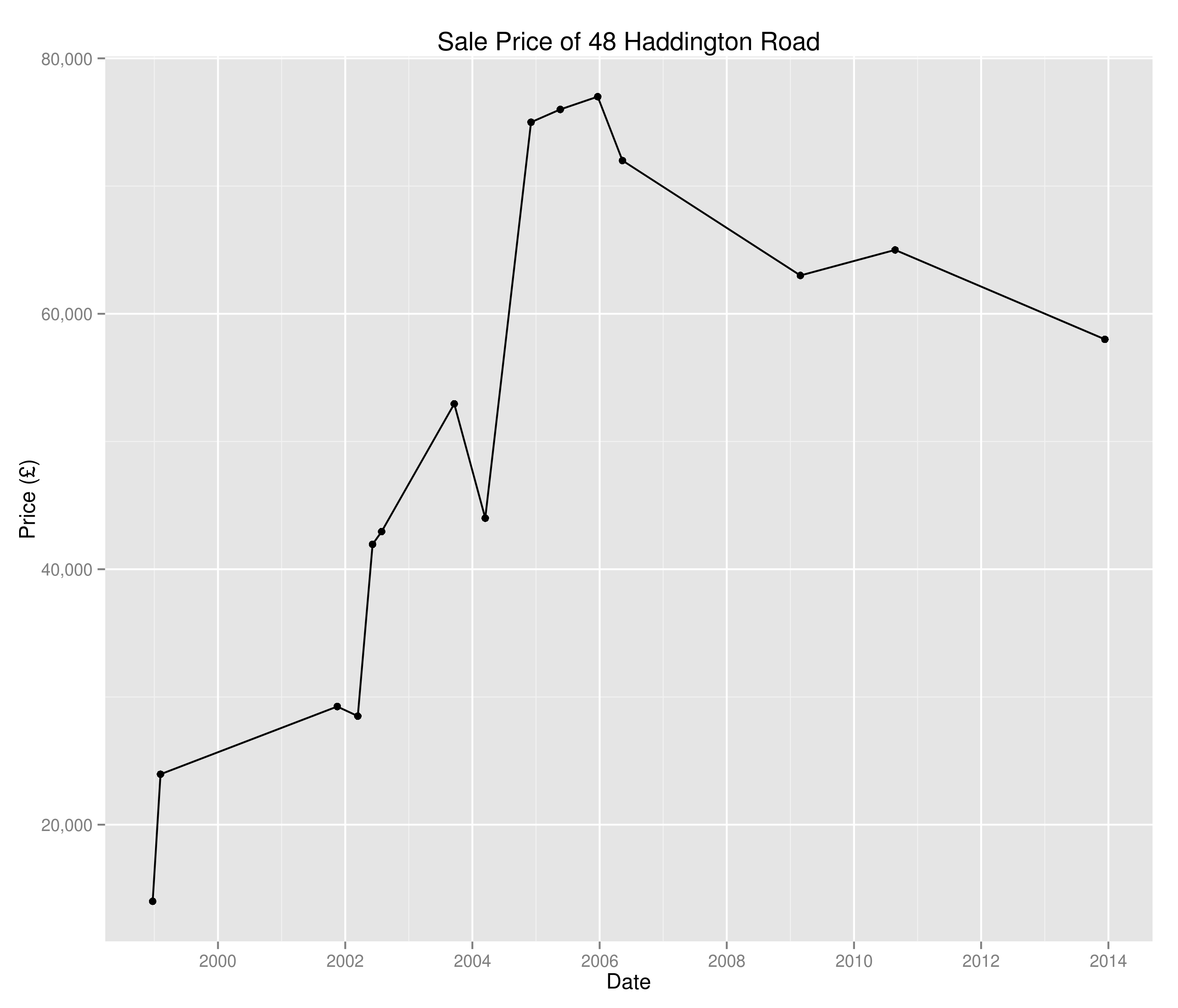
Quite a lot of work, really, just to generate some ‘likely looking’ sales data. Again, if you’ve got your own then use it! However, up till now I’ve just asserted that it’s likely looking. If you play around with it you can actually see some pretty interesting stuff. Firstly, with lots and lots of data point (N = 8000) you see that the company revenue growth looks very exponential:
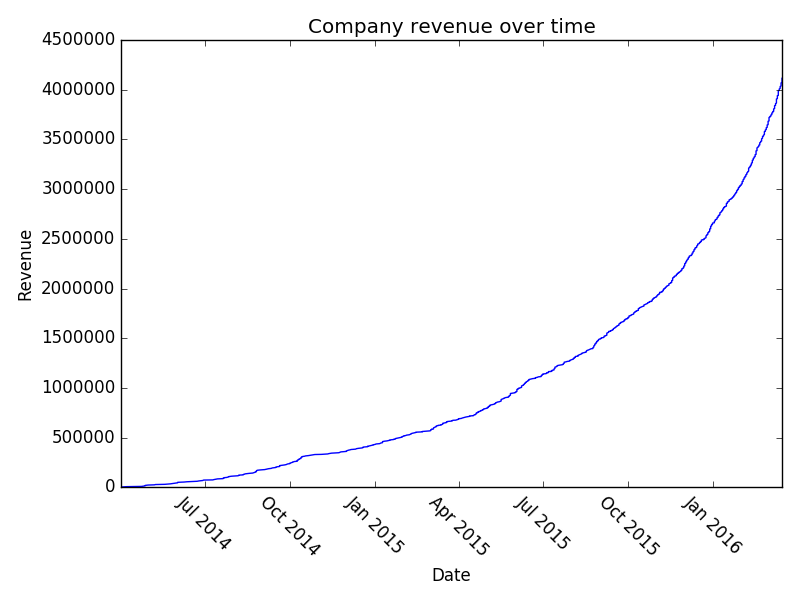
However, it’s unlikely that you’ve got 8000 B2B transactions in your sales pipeline (if you do, kudos!). Let’s examine the situation where you’ve got 150:
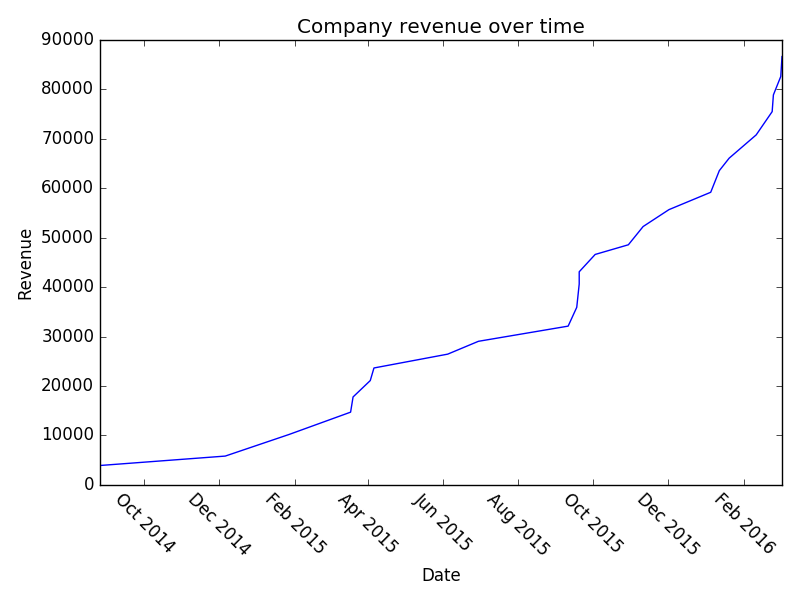
And a once more with 150:
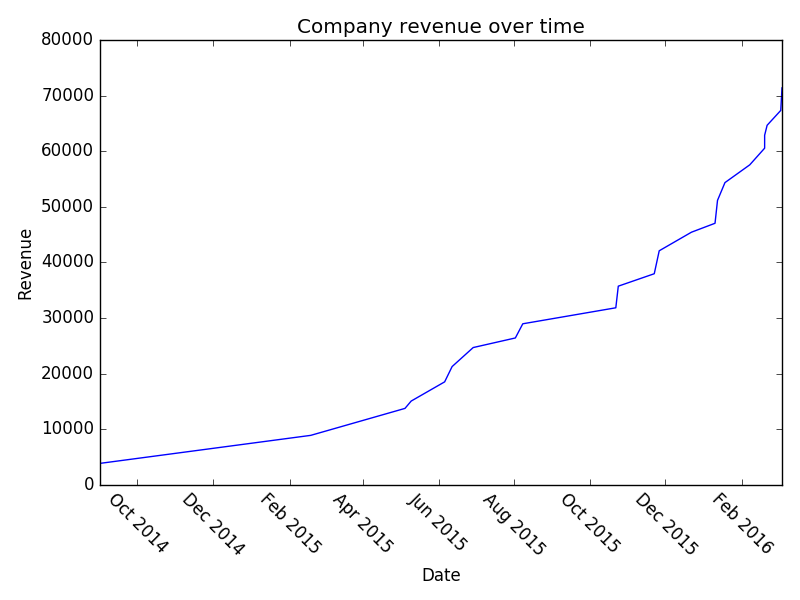
I think it’s interesting that, even though we’ve literally built this whole pipeline using exponential growth – we still look flat in a lot of places. Hopefully that might provide some solace if you’re struggling with sales and think you’re not hitting your exponential growth. Play around with the parameters and you can see what sort of effect increasing your conversion at various stages has on your overall revenue etc. Or just read the company names – they’re also pretty good.
Right, I’m counting that as broadly done. We’ve got sales data that nobody will mind me analysing in a public forum. Stay tuned/subscribe/email me to keep in touch for part 2. We’ll imagine that we’ve started with this data and we’ll try to assign a total value to our pipeline, and maybe even get onto predicting how many opportunities will progress in the next N days.